翻译勾八

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，它们分别含有 n 和 m 个元素。请你计算以下两个数值：

  • answer1：使得 nums1[i] 在 nums2 中出现的下标 i 的数量。

  • answer2：使得 nums2[i] 在 nums1 中出现的下标 i 的数量。

返回 [answer1, answer2]。

示例 1：

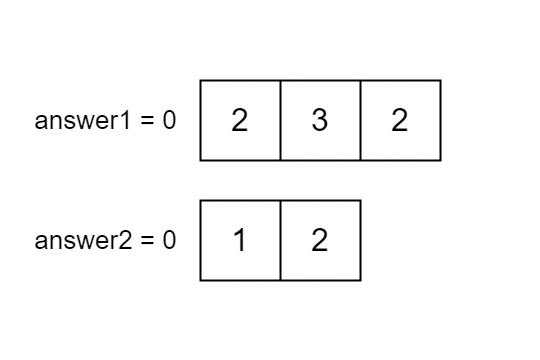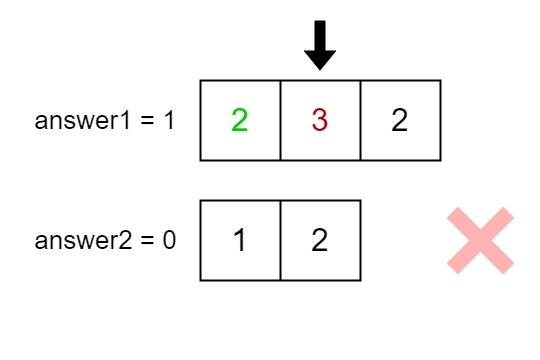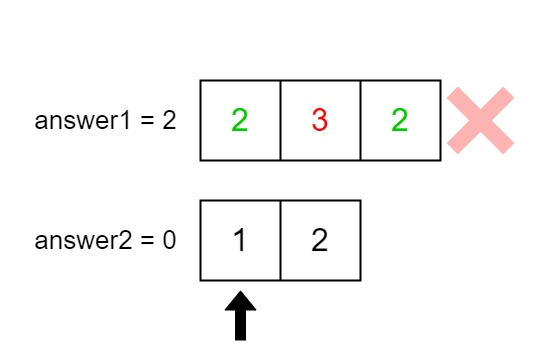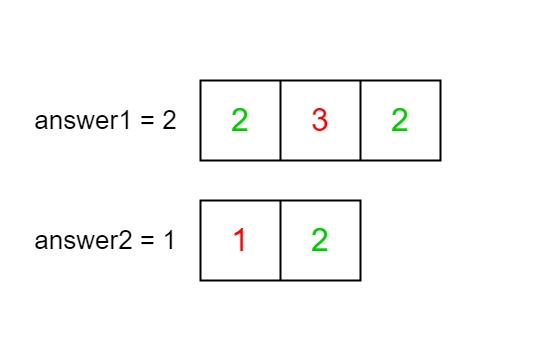
输入：nums1 = [2,3,2], nums2 = [1,2]

输出：[2,1]

解释：

示例 2：

输入：nums1 = [4,3,2,3,1], nums2 = [2,2,5,2,3,6]

输出：[3,4]

解释：

nums1 中下标在 1，2，3 的元素在 nums2 中也存在。所以 answer1 为 3。

nums2 中下标在 0，1，3，4 的元素在 nums1 中也存在。所以 answer2 为 4。

示例 3：

输入：nums1 = [3,4,2,3], nums2 = [1,5]

输出：[0,0]

解释：

nums1 和 nums2 中没有相同的数字，所以答案是 [0,0]。

 提示：

  • n == nums1.length

  • m == nums2.length

  • 1 <= n, m <= 100

  • 1 <= nums1[i], nums2[i] <= 100

思路

  • 取小长度数组统计

  • 优化(数组长度最大为100，常数级别)

  • 减少二次循环：个十百位统计nums1，千万十万位统计nums2，相互存在才计数，所以在r2==0时直接加上nums1中存在的所有数量，之后不计算

代码

  • 取小长度数组统计

class Solution {
    public int[] findIntersectionValues(int[] nums1, int[] nums2) {
        int result1 = 0;
        int result2 = 0;
        boolean[] b1 = new boolean[101];
        boolean[] b2 = new boolean[101];
        if(nums1.length < nums2.length){
            for(int num : nums1){
                b1[num]=true;
            }
            for(int num : nums2){
                if(b1[num]){
                    result2++;
                }
                b2[num]=true;
            }
            for(int num : nums1){
                if(b2[num]){
                    result1++;
                }
            }
        }else{
            for(int num : nums2){
                b2[num]=true;
            }
            for(int num : nums1){
                if(b2[num]){
                    result1++;
                }
                b1[num]=true;
            }
            for(int num : nums2){
                if(b1[num]){
                    result2++;
                }
            }
        }
        return new int[]{result1, result2};
    }
}

  • 优化

class Solution {
    public int[] findIntersectionValues(int[] nums1, int[] nums2) {
        int result1 = 0;
        int result2 = 0;
        boolean[] b1 = new boolean[101];
        boolean[] b2 = new boolean[101];
        for (int num : nums1) {
            b1[num] = true;
        }
        for (int num : nums2) {
            if (b1[num]) {
                result2++;
            }
            b2[num] = true;
        }
        for (int num : nums1) {
            if (b2[num]) {
                result1++;
            }
        }
        return new int[]{result1, result2};
    }
}

  • 减少二次循环

class Solution {
    public int[] findIntersectionValues(int[] nums1, int[] nums2) {
        int r1 = 0;
        int r2 = 0;
        int[] counts = new int[101];
        for (int num : nums1) {
            counts[num]++;
        }
        for (int num : nums2) {
            if (counts[num] % 1000 != 0) {
                r2++;
                if (counts[num] / 1000 == 0) {
                    r1 += counts[num] % 1000;
                }
                counts[num] += 1000;
            }
        }
        return new int[]{r1, r2};
    }
}